Problem link: https://onlinejudge.org/index.php?option=onlinejudge&Itemid=8&page=show_problem&problem=1119

Note:

This problem mainly comprises one main concern – calculating the faces. Now there is already a famous formula – Euler’s formula for calculating the number of faces in a planar graph which is

Here, v = total number of vertices of all the connected components of the planar graph

e = total number of edges of all the connected components of the planar graph

f = number of faces (regions bounded by edges, including the outer, infinitely large region) of the planar graph

Since we want the faces for this problem, the equation we should be looking for is:

f = 2 + e − v …………………………………………………………… (1)

Now, at this point it is seeming pretty easy to get the number of faces, right? Because we just need only the number of vertices and edges and nothing else!! But here goes the main concern – The above equation is assuming there is only one connected component in the planar graph. So if the overall graph is not connected, that means, if, in the plane, we are talking about multiple subgraphs that are disconnected from each other, then we’ll have to apply the above equation for each of the connected components to get the total number of faces, right?

But again, in that case (more than 1 connected component), there is another certain issue – the face counter for the outer region gets counted equal to the number of different connected component, which actually should be counted as 1.

For example: Suppose we are considering the below graphs as the input of our problem.

Here, in the plane, the number of connected components is 2 (A-B-C-D and E-F-G-H) and the above equation will generate the number of faces for each connected component as 2, so in total 4 faces for the graphs present in this plane. But the result should be 3 instead of 4.

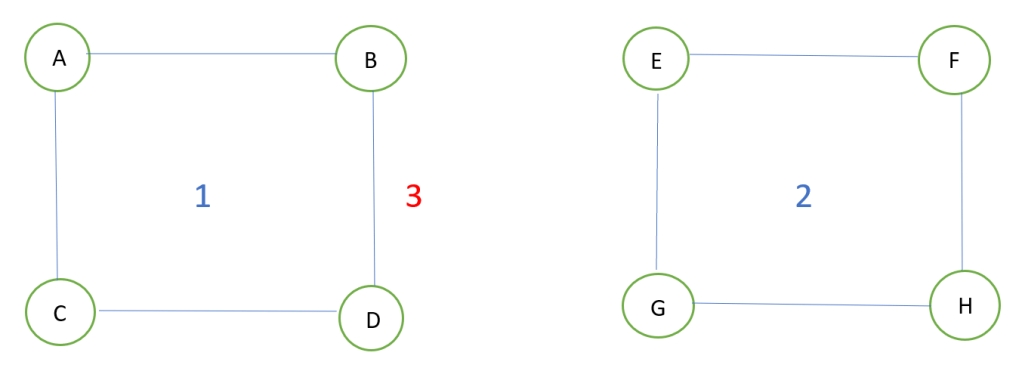
So the thing is that, we should consider only 1 face for the enitre infinite outer region for all the different connected components. So the equation for our problem would be modified to:

f = ( e − v + number of connected components ) + 1 …………………………. (2)

This will be applicable because we can easily derive that, if we make summation of each connected component, then we can reach to the above equation for considering only 1 outer region for all the connected components present in the plane.

Now the solution to the problem comes down to the two following steps:

1. Find out the number of connected components (/ number of cycles in the undirected graph) in the graph that is given to us
2. Put that into the modified Euler’s equation (2) to get the result.

The first part of the solution can be solved in many different ways like DFS or Disjoint set. I have used the Disjoint set algorithm here.

Code:

#include <bits/stdc++.h>

using namespace std;

int Find(int x, vector<int> &root)
{
    if(x==root[x]) return x;
    return root[x]=Find(root[x], root); //Path compression
}

void Union(int x, int y, vector<int> &root, vector<int> &ranking)
{
    int rootX=Find(x, root);
    int rootY=Find(y, root);
    if(rootX!=rootY)
    {
        if(ranking[rootX]>=ranking[rootY])
        {
            root[rootY]=rootX;
            ranking[rootX]+=ranking[rootY];
        }
        else
        {
            root[rootX]=rootY;
            ranking[rootY]+=ranking[rootX];
        }
    }
}


int main()
{
//    freopen("in.txt","r",stdin);
//    freopen("out.txt","w",stdout);
    int node, edge;
    while(cin>>node>>edge)
    {
        vector<int> root(node+1), ranking(node+1);
        for(int i=1; i<=node; i++)
        {
            root[i]=i;
            ranking[i]=1;
        }
        unordered_map<char, int> ump;
        int c=0;
        for(int i=0; i<edge; i++)
        {
            char a,b;
            cin>>a>>b;
            if(!ump.count(a))
            {
                c++;
                ump[a]=c;
            }
            if(!ump.count(b))
            {
                c++;
                ump[b]=c;
            }

            int x=ump[a];
            int y=ump[b];
            Union(x, y, root, ranking);
        }

        int faces=0;
        for(int i=1; i<=node; i++)
        {
            if(root[i]==i) faces++;
        }
        cout<<(edge-node+faces)+1<<endl; //the +1 is for 1 infinite outer region
    }
    return 0;
}