Solution Technique:
Since matrix exponentiation is all about just forming the 3 matrices,so if once formed correctly, the problem is solved. Who those are new in matrix expo solving, for them one thing in this problem is important that, after reading the statement you may think of making two different matrices and seperately run matrix expo on them. But that is inconvenient because of much complexity, so you have to make only one matrix and have to do work with that matrix. That is convenient and more flexible for applying matrix expo. The solution matrix for the problem is –
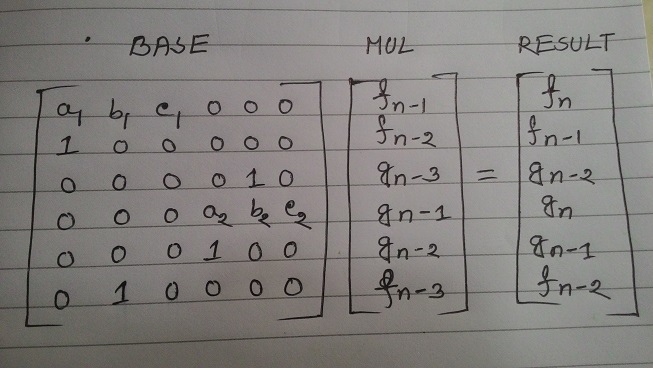
I have arranged my matrix in this way but there can be several form of this matrix. But the logic should be correct.
But the logic should be correct during building the matrices. That's all.
Solution:
#include <bits/stdc++.h>
#define pf printf
#define sf(a) scanf("%d",&a)
#define sfl(a) scanf("%lld",&a)
#define sff(a,b) scanf("%d %d",&a,&b)
#define sffl(a,b) scanf("%lld %lld",&a,&b)
#define sfff(a,b,c) scanf("%d %d %d",&a,&b,&c)
#define sfffl(a,b,c) scanf("%lld %lld %lld",&a,&b,&c)
#define sffff(a,b,c,d) scanf("%d %d %d %d",&a,&b,&c,&d)
#define sffffl(a,b,c,d) scanf("%lld %lld %lld %lld",&a,&b,&c,&d)
#define sfffff(a,b,c,d,e) scanf("%d %d %d %d %d",&a,&b,&c,&d,&e)
#define sfffffl(a,b,c,d,e) scanf("%lld %lld %lld %lld %lld",&a,&b,&c,&d,&e)
#define sfc(a) scanf("%c",&a)
#define ms(a,b) memset(a,b,sizeof(a))
#define pb(a) push_back(a)
#define pbp(a,b) push_back({a,b})
#define db double
#define ft float
#define ll long long
#define ull unsigned long long
#define ff first
#define ss second
#define sz(x) x.size()
#define qu queue
#define pqu priority_queue
#define vc vector
#define vi vector<int>
#define vll vector<long long>
#define pii pair<int,int>
#define pis pair<int,string>
#define psi pair<string,int>
#define all(x) x.begin(),x.end()
#define CIN ios_base::sync_with_stdio(0); cin.tie(0)
#define max3(a, b, c) max(a, b) > max(b, c) ? max(a, b) : max(b, c)
#define min3(a, b, c) min(a, b) < min(b, c) ? min(a, b) : min(b, c)
#define loop0(i,n) for(int i=0;i<n;i++)
#define loop1(i,n) for(int i=1;i<=n;i++)
#define loopcmp(i,n) for(int i=1;i<n;i++)
#define looprev(i,n) for(int i=n-1; i>=0; i--)
#define loopab(i,a,b) for(int i=a;i<=b;i++)
#define loopba(i,b,a) for(int i=b;i>=a;i--)
#define stlloop(x) for(__typeof(x.begin()) it=x.begin();it!=x.end();it++)
#define gcd(a, b) __gcd(a, b)
#define lcm(a, b) ((a)*((b)/gcd(a,b)))
#define case1(z) cout<<"Case "<<z<<":"<<endl
#define case2(z) printf("Case %d: ",z)
#define PI acos(-1) //3.14159265358979323846264338328
#define valid(tx,ty) tx>=0 && tx<row && ty>=0 && ty<col
#define intlim 2147483648
#define MAX 1000000
#define inf 100000000
/*------------------------------Graph Moves----------------------------*/
//const int fx[]={+1,-1,+0,+0};
//const int fy[]={+0,+0,+1,-1};
//const int fx[]={+0,+0,+1,-1,-1,+1,-1,+1}; // Kings Move
//const int fy[]={-1,+1,+0,+0,+1,+1,-1,-1}; // Kings Move
//const int fx[]={-2, -2, -1, -1, 1, 1, 2, 2}; // Knights Move
//const int fy[]={-1, 1, -2, 2, -2, 2, -1, 1}; // Knights Move
/*---------------------------------------------------------------------*/
using namespace std;
/*----------------------Matrix-----------------------*/
ll MOD;
struct matrix
{
ll mat[6][6];
int row,col;
matrix()
{
ms(mat,0);
}
matrix(int a, int b)
{
row=a,col=b;
ms(mat,0);
}
matrix operator*(const matrix &p) const
{
//assert(col == p.row);
matrix result;
result.row = row;
result.col = p.col;
for (int i = 0; i < result.row; i++)
{
for (int j = 0; j < result.col; j++)
{
ll sum = 0;
for (int k = 0; k <col; k++)
{
sum += ((mat[i][k]%MOD) * (p.mat[k][j]%MOD))%MOD;
sum%=MOD;
}
result.mat[i][j] = sum;
}
}
return result;
}
matrix operator+ (const matrix &p) const
{
assert(row==p.row && col==p.col);
matrix result;
result.row=row;
result.col=col;
for(int i=0; i<result.row; i++)
{
for(int j=0; j<result.col; j++)
result.mat[i][j]=((mat[i][j]%MOD)+(p.mat[i][j]%MOD))%MOD;;
}
return result;
}
matrix identity()
{
matrix result;
result.row=row;
result.col=col;
for(int i=0; i<row; i++)
result.mat[i][i]=1;
return result;
}
matrix pow(ll pow)
{
matrix result=(*this);
matrix ret=(*this).identity();
while(pow)
{
if(pow % 2==1)
ret=ret*result;
result=result*result;
pow/=2;
}
return ret;
}
void show()
{
printf("-----------------------------\n");
for(int i=0; i<row; i++)
{
for(int j=0; j<col; j++)
printf("%lld ",mat[i][j]);
printf("\n");
}
printf("-----------------------------\n");
}
};
ll power(ll n,ll p)
{
if(p==0) return 1;
ll r=1;
for(int i=0; i<p; i++) r*=n;
return r;
}
/*--------------------------Matrix End---------------------*/
int main()
{
///freopen("in.txt","r",stdin);
///freopen("out.txt","w",stdout);
ll a1,b1,c1,a2,b2,c2,f0,f1,f2,g0,g1,g2,m,q,n,t;
sfl(t);
loop1(z,t)
{
sfffl(a1,b1,c1);
sfffl(a2,b2,c2);
sfffffl(f0,f1,f2,g0,g1);
sfffl(g2,m,q);
MOD=m;
matrix base(6,6),mul(6,1),result(6,6);
base.mat[0][0]=a1%MOD;
base.mat[0][1]=b1%MOD;
base.mat[0][2]=c1%MOD;
base.mat[3][3]=a2%MOD;
base.mat[3][4]=b2%MOD;
base.mat[3][5]=c2%MOD;
base.mat[1][0]=base.mat[2][4]=base.mat[4][3]=base.mat[5][1]=1;
mul.mat[0][0]=f2%MOD;
mul.mat[1][0]=f1%MOD;
mul.mat[2][0]=g0%MOD;
mul.mat[3][0]=g2%MOD;
mul.mat[4][0]=g1%MOD;
mul.mat[5][0]=f0%MOD;
case1(z);
loop0(i,q)
{
sfl(n);
result=base.pow(n-2);
result=result*mul;
ll rs1=result.mat[0][0];
ll rs2=result.mat[3][0];
if(n==0)
{
rs1=f0%MOD;
rs2=g0%MOD;
}
else if(n==1)
{
rs1=f1%MOD;
rs2=g1%MOD;
}
else if(n==2)
{
rs1=f2%MOD;
rs2=g2%MOD;
}
cout<<rs1<<" "<<rs2<<endl;
}
}
return 0;
}