This problem is simply the theorem 3.10 of Higher Geometry – class 9-10 !! 😀

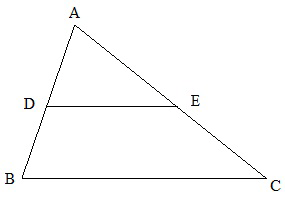
Let ADE / BDEC = x/y .
So ADE / ABC = x/(x+y)
From the theorem,we know that,

ADE / ABC = DE^2 / BC^2
or, sqrt (ADE / ABC) = DE/BC
or, sqrt (x/(x+y)) = DE/BC
or, r = DE/BC where r = sqrt(m)/sqrt((m+n))

As ADE and ABC are similar triangle, so

AD/AB = DE /BC
or, AD = DE/BC* AB
or, AD = r * AB .

Thus, the value of AD can be found simply by using the above formula.
NOTE: This problem also can be solved by “bisection” or other method if you don’t wanna bother remembering the formula.

#include <bits/stdc++.h>

#define pf                  printf
#define sf(a)               scanf("%d",&a)
#define sfl(a)              scanf("%lld",&a)
#define sff(a,b)            scanf("%d %d",&a,&b)
#define sffl(a,b)           scanf("%lld %lld",&a,&b)
#define sfff(a,b,c)         scanf("%d %d %d",&a,&b,&c)
#define sfffl(a,b,c)        scanf("%lld %lld %lld",&a,&b,&c)
#define sffff(a,b,c,d)      scanf("%d %d %d %d",&a,&b,&c,&d)
#define sffffl(a,b,c,d)     scanf("%lld %lld %lld %lld",&a,&b,&c,&d)
#define sfffff(a,b,c,d,e)   scanf("%d %d %d %d %d",&a,&b,&c,&d,&e)
#define sfffffl(a,b,c,d,e)  scanf("%lld %lld %lld %lld %lld",&a,&b,&c,&d,&e)
#define sfc(a)              scanf("%c",&a)
#define ms(a,b)             memset(a,b,sizeof(a))
#define pb(a)               push_back(a)
#define pbp(a,b)            push_back({a,b})
#define db                  double
#define ft                  float
#define ll                  long long
#define ull                 unsigned long long
#define ff                  first
#define ss                  second
#define sz(x)               x.size()
#define qu                  queue
#define pqu                 priority_queue
#define vc                  vector
#define vi                  vector<int>
#define vll                 vector<long long>
#define pii                 pair<int,int>
#define pis                 pair<int,string>
#define psi                 pair<string,int>
#define all(x)              x.begin(),x.end()
#define CIN                 ios_base::sync_with_stdio(0); cin.tie(0)
#define max3(a, b, c)       max(a, b) > max(b, c) ? max(a, b) : max(b, c)
#define min3(a, b, c)       min(a, b) < min(b, c) ? min(a, b) : min(b, c)
#define loop0(i,n)          for(int i=0;i<n;i++)
#define loopn(i,n)          for(int i=1;i<n;i++)
#define loop1(i,n)          for(int i=1;i<=n;i++)
#define loopi(i,n)          for(int i=0;i<n-1;i++)
#define loopab(i,a,b)       for(int i=a;i<=b;i++)
#define loopba(i,b,a)       for(int i=b;i>=a;i--)
#define REV(i,n)            for(i=n; i>=0; i--)
#define stlloop(x)          for(__typeof(x.begin()) it=x.begin();it!=x.end();it++)
#define gcd(a, b)           __gcd(a, b)
#define lcm(a, b)           ((a)*((b)/gcd(a,b)))
#define case1(z)            cout<<"Case "<<z<<": "
#define case2(z)            printf("Case %d: ",z)
#define PI                  3.14159265358979323846264338328
#define valid(tx,ty)        tx>=0 && tx<row && ty>=0 && ty<col
#define intlim              2147483648
#define MAX                 1000000
#define inf                 100000000

/*------------------------------Graph Moves----------------------------*/
//const int fx[]={+1,-1,+0,+0};
//const int fy[]={+0,+0,+1,-1};
//const int fx[]={+0,+0,+1,-1,-1,+1,-1,+1};   // Kings Move
//const int fy[]={-1,+1,+0,+0,+1,+1,-1,-1};  // Kings Move
//const int fx[]={-2, -2, -1, -1,  1,  1,  2,  2};  // Knights Move
//const int fy[]={-1,  1, -2,  2, -2,  2, -1,  1}; // Knights Move
/*---------------------------------------------------------------------*/

using namespace std;

int main()
{
    //CIN;
    //freopen("in.txt","r",stdin);
    //freopen("out.txt","w",stdout);
    int t;
    sf(t);
    loop1(z,t)
    {
        double AB,AC,BC,rat,x,AD;
        cin>>AB>>AC>>BC>>rat;
        x=sqrt((rat)/(rat+1)); // ADE/ABC=DE^2/BC^2 AND Here, ADE/ABC=(rat)/(rat+1) and x^2=DE^2/BC^2
        AD=x*AB;
        case2(z);
        pf("%.6f\n",AD);
    }
    return 0;
}